After a rally against the market, here’s why NEAR can breach $20 next week

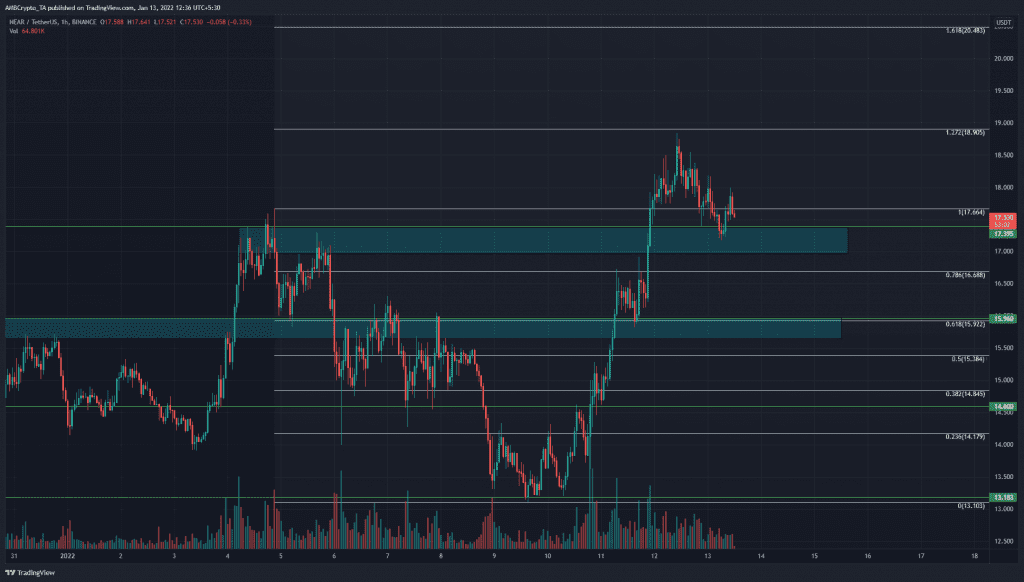
Over the past few days, NEAR Protocol has rallied impressively from the lows at $13.18. Bitcoin has also bounced from the $40.5k support, and NEAR has been able to climb past areas of supply with relative ease. The rally upward provided some short-term targets as take-profit levels for bulls.

Over the past two weeks, the price has found strong support at the $13.1 level. Using NEAR’s move from $17.664 down to $13.183, Fibonacci retracement and extension levels (white) were plotted. The 27.2% level at $18.9 was missed by a small margin, and NEAR saw a pullback from $18.8 down to the $17.3 area of former supply.

This retest flipped it from a supply zone to a demand zone. This was particularly important because, in the past two weeks, NEAR has bounced between the $15.9 and $13.2 levels for the most part.

Having tested the $17.4 area in search of demand and finding buyers, it appeared likely that NEAR would move upward once again. the 61.8% extension level presented a target of $20.48 for NEAR to achieve over the next few days.

Rationale

Source: NEAR/USDT on TradingView

The hourly RSI was back at neutral 50 after the pullback. It was likely that the RSI would climb once more, as the previous highs have been taken out and were retested to find buyers. A note of caution, perhaps, would be slightly low trading volumes upon the retest.

The CMF had been well above +0.05 on the move up for NEAR but was near -0.05 at the time of writing. This showed that capital flow was directed out of the market, but not significantly so.

Conclusion

The indicators showed some bullish strength behind NEAR, but the price action was far more convincing. It appeared likely that NEAR would move toward $20.5 in the short term. However, NEAR could also see a move back to $15.9 in a hunt for liquidity. Such a move would force late longs to close at a loss, would encourage short-sellers, and overall provide market makers more ammunition to drive NEAR higher on the back of volatility once more. Hence, although the market structure was bullish, a retest of $15.9 before a move to $20 won’t be impossible.